https://www.acmicpc.net/problem/11505
11505번: 구간 곱 구하기
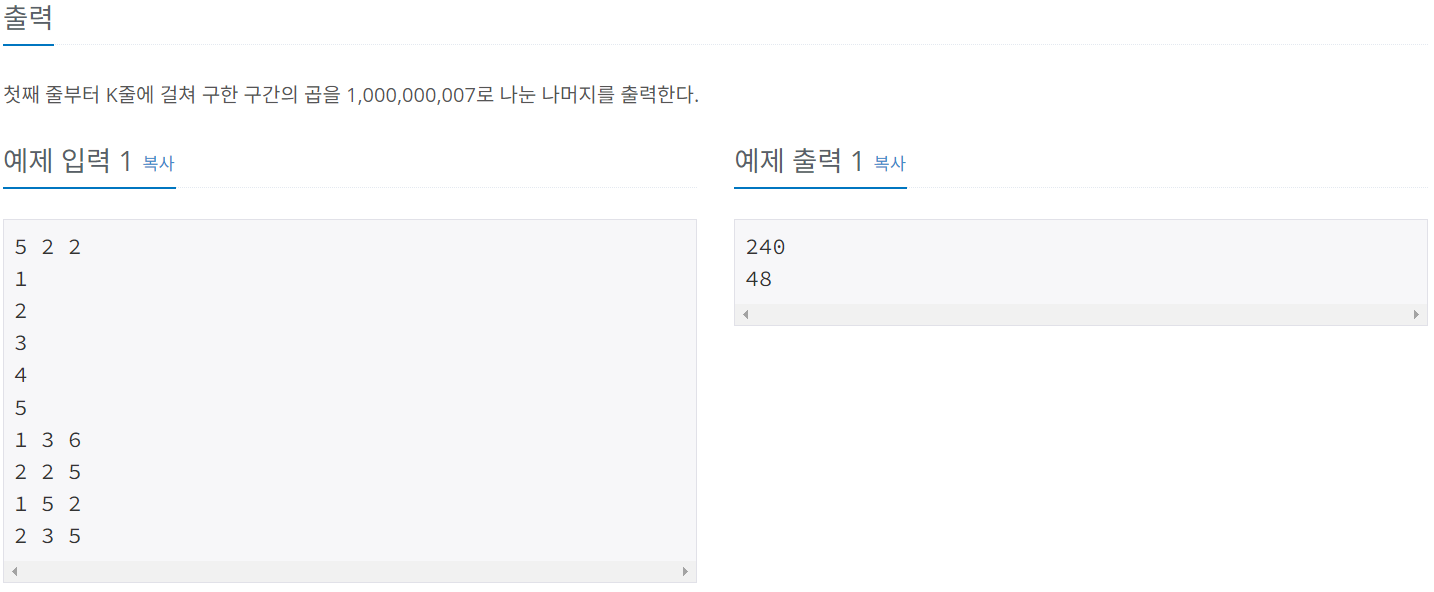
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 곱을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net

사용한 알고리즘 : 세그먼트 트리
풀이전략
만약 완전 탐색을 통해 문제를 푼다고 생각해보자.
그러면 최악의 경우, 수의 개수 N = 1,000,000 , 수 변경 횟수 M = 10,000, 구간 곱 구하는 횟수 K = 10,000으로
1,000,000 * (10,000+10,000) = 20,000,000,000(200억)번의 연산이 필요하다.
JAVA는 초당 1억번의 연산을 수행하므로 200초의 시간이 소요되는 것이다.
하지만 주어진 시간 제한은 1초로 시간 초과가 발생한다.
따라서 우리는 더 효율적인 연산을 수행할 수 있어야한다.
그런 연산을 수행하는 적합한 알고리즘으로 세그먼트 트리가 있다.
세그먼트 트리는 특정 구간에서의 합, 최댓값, 최솟값, 곱 등의 연산을 빠르게 수행하기 때문이다.
세그먼트 트리에서 특정 값 수정에 걸리는 시간 복잡도는 O(logN),
구간의 질의(구간합, 구간곱, 구간 최댓값 등)를 구하는데 걸리는 시간 복잡도는 O(logN)으로
최악의 경우, 수의 개수 N = 1,000,000 , 수 변경 횟수 M = 10,000일 때
1,000,000 * log(10,000+10,000) = 1,000,000 * 14.287712 = 약 14,287,712(1400만)번 연산이 필요하다.
이는 JAVA가 약 0.14초면 연산해낼 수 있으며, 완전 탐색 방법을 사용했을 때보다 1428배 이상 빠르다.
(만약 수가 더 커질 수 있다면 커질수록 차이가 많이 날 것이다.)
이 문제에서는 기본적인 세그먼트 트리 알고리즘 템플릿을 사용하면 풀 수 있는 문제이다.
다만 특정 트리의 노드가 가지고 있는 값이, 양쪽 자식 노드의 값의 곱셈으로 이루어져있다.
세그먼트 트리 개념과 코드 설명에 대한 내용은 위 링크에 정리해두었으니 필요하면 참고바란다.
제출코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int arr[];
static long tree[];
static long divideVal=1000000007L;
static long init_tree(int index, int nodeLeft, int nodeRight){
if(nodeLeft==nodeRight) return tree[index]=arr[nodeLeft];
int mid = (nodeLeft+nodeRight)/2;
long left = init_tree(index*2,nodeLeft,mid);
long right = init_tree(index*2+1,mid+1,nodeRight);
return tree[index]=(left*right)%divideVal;
}
static long modify_tree(int index, int newVal, int node, int nodeLeft, int nodeRight){
if(index<nodeLeft || index>nodeRight) return tree[node];
if(nodeLeft==nodeRight) return tree[node]=newVal;
int mid = (nodeLeft+nodeRight)/2;
long left = modify_tree(index,newVal,node*2,nodeLeft,mid);
long right = modify_tree(index,newVal,node*2+1,mid+1,nodeRight);
return tree[node]=(left*right)%divideVal;
}
static long query_tree(int start, int end, int node, int nodeLeft, int nodeRight){
if(start>nodeRight || end<nodeLeft) return 1;
if(start<=nodeLeft && nodeRight<=end) return tree[node];
int mid = (nodeLeft+nodeRight)/2;
long left = query_tree(start,end,node*2,nodeLeft,mid);
long right = query_tree(start,end,node*2+1,mid+1,nodeRight);
return (left*right)%divideVal;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
arr = new int[N+1];
tree = new long[4*N];
for(int i=1;i<=N;++i){
arr[i]=Integer.parseInt(br.readLine());
}
init_tree(1,1,N);
for(int i=0;i<M+K;++i){
st = new StringTokenizer(br.readLine());
int command = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
if(command==1){
modify_tree(a,b,1,1,N);
}
else{
bw.write(query_tree(a,b,1,1,N)+"\n");
}
}
bw.flush();
bw.close();
}
}
