[BOJ 16724] 피리 부는 사나이 - JAVA, Gold3
https://www.acmicpc.net/problem/16724
16724번: 피리 부는 사나이
첫 번째 줄에 지도의 행의 수를 나타내는 N(1 ≤ N ≤ 1,000)과 지도의 열의 수를 나타내는 M(1 ≤ M ≤ 1,000)이 주어진다. 두 번째 줄부터 N개의 줄에 지도의 정보를 나타내는 길이가 M인 문자열이 주
www.acmicpc.net



사용한 알고리즘 : 분리 집합, DFS
풀이 전략
문제에서는 회원들이 발판을 따라 움직인다고 할 때,
회원들이 반복되는 싸이클로 인해 계속해서 발판을 움직이며 돌지않고
중간에 멈출 수 있도록 SAFE ZONE을 만드려고 한다.
이 때 이를 만족시킬 수 있는 SAFE ZONE의 최소 개수를 구하는 것이 목표이다.
풀이 방법이 여러가지 있겠지만, 나는 분리 집합과 DFS를 사용하여 풀이했다.
DFS 탐색을 통해 주어진 발판 입력에 따라 그래프 탐색을 진행하고,
탐색 진행과정에서 거쳐가는 발판들을 모두 하나의 집합으로 묶는다.
이 때, 하나의 집합마다 회원들이 싸이클을 반복해서 돌지않도록 하나의 SAFE ZONE을 만들어주면 된다.
즉, (DFS 탐색간 생성되는 집합의 개수) = (최소로 필요한 SAFE ZONE의 개수)인 것이다.
위 문제에서 주어진 예제입력을 그림으로 표현하면 아래와 같다.
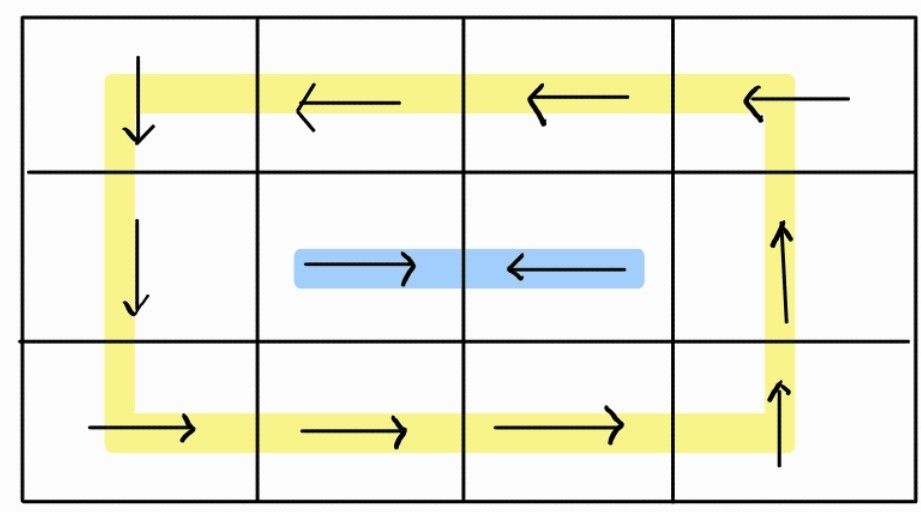
사이클이 반복되는 집합이 2개 있는 것을 알 수 있다.
따라서 이 예제에서 최소로 필요한 SAFE ZONE은 2개이다.
만약 2행 2열의 '→'가 '←'로 변한다면 집합은 아래 그림과 같이 1개로, 최소로 필요한 SAFE ZONE 또한 1개가 된다.

위의 풀이 전략 구현을 위한 중요 알고리즘으로 아래 두 메서드가 있다.
static int find_parent(int x, int y){
if(parent[x][y]==M*x+y) return M*x+y;
else return parent[x][y]=find_parent(parent[x][y]/M,parent[x][y]%M);
}
static void union_parent(int aX, int aY, int bX, int bY){
int A = find_parent(aX,aY);
int B = find_parent(bX,bY);
if(A<B) parent[B/M][B%M]=A;
else parent[A/M][A%M]=B;
}이들은 분리 집합을 구현하는 메서드들로
첫번째는 특정 좌표의 최상위 부모 번호를 구하는 메서드이고,
두번째는 DFS 탐색간 이동 전 좌표와 이동 후 좌표가 가지는 각각의 최상의 부모 번호를 구하고
더 큰 번호를 가진 좌표가 최상위 부모 번호를 더 작은 번호로 변경하는 메서드이다.(같은 집합으로 만들어 주는 메서드)
여기서 특정 좌표 둘의 최상위 부모 번호가 동일하다는 것은 같은 집합에 속한다는 것을 의미한다.
이들 메서드에서 주의해야 할 부분은 find_parent(parent[x][y]/M,parent[x][y]%M);와
if(A<B) parent[B/M][B%M]=A; else parent[A/M][A%M]=B;인데 왜 이런 수식을 갖는지 아래에 설명하겠다.
(M은 입력으로 주어진 2차원 배열의 열 길이를 뜻한다. 아래 그림에서 M=4)
처음 좌표별 최상위 부모 번호를 담은 배열은 아래와 같이 정의된다.

먼저 find_parent(parent[x][y]/M,parent[x][y]%M);에서
x,y 좌표의 부모 번호인 parent[x][y]가 5라고 가정해보자.
그리고 우리는 parent[x][y] (=5)의 좌표 번호를 알아야 하는데
parent[x][y]의 x좌표는 5/m을 한 1, y좌표는 5%m을 한 1이 나와 (1,1)에 위치함을 알 수 있다.
따라서 (x,y) 좌표에서의 부모 번호인 parent[x][y]가 있는 좌표를 구하기 위해 find_parent(parent[x][y]/M,parent[x][y]%M);로
수식을 작성한 것이다.
union_parent 메서드에서의 if(A<B) parent[B/M][B%M]=A; else parent[A/M][A%M]=B;도 비슷한 맥락으로
부모 노드의 x,y 좌표를 나타내기 위해 배열 내 인덱스를 위같이 정의한 것이다.
그리고 모든 좌표가 가지는 최상위 부모 번호를 set 컬렉션을 이용해 중복을 없애 남는
set의 size를 구하면 우리가 목표한 SAFE ZONE의 최소 개수가 출력된다.
제출코드
import java.io.*;
import java.util.HashSet;
import java.util.Set;
import java.util.StringTokenizer;
public class Main{
static int N,M;
static char graph[][];
static boolean visited[][];
static int parent[][];
static int find_parent(int x, int y){
if(parent[x][y]==M*x+y) return M*x+y;
else return parent[x][y]=find_parent(parent[x][y]/M,parent[x][y]%M);
}
static void union_parent(int aX, int aY, int bX, int bY){
int A = find_parent(aX,aY);
int B = find_parent(bX,bY);
if(A<B) parent[B/M][B%M]=A;
else parent[A/M][A%M]=B;
}
static void dfs(int x,int y){
// 두 좌표가 같은 집합에 속하지 않는 경우에만 탐색을 진행한다.
if(graph[x][y]=='U' && find_parent(x,y)!=find_parent(x-1,y)){
union_parent(x,y,x-1,y);
dfs(x-1,y);
}
else if(graph[x][y]=='D' && find_parent(x,y)!=find_parent(x+1,y)){
union_parent(x,y,x+1,y);
dfs(x+1,y);
}
else if(graph[x][y]=='L' && find_parent(x,y)!=find_parent(x,y-1)){
union_parent(x,y,x,y-1);
dfs(x,y-1);
}
else if(graph[x][y]=='R' && find_parent(x,y)!=find_parent(x,y+1)){
union_parent(x,y,x,y+1);
dfs(x,y+1);
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
graph = new char[N][M];
visited = new boolean[N][M];
parent = new int[N][M];
for(int i=0;i<N;++i){
for(int j=0;j<M;++j){
parent[i][j]=i*M+j;
}
}
for(int i=0;i<N;++i){
String str = br.readLine();
for(int j=0;j<M;++j){
graph[i][j]=str.charAt(j);
}
}
if(N==1 && M==1){
bw.write("1\n");
bw.flush();
bw.close();
return;
}
for(int i=0;i<N;++i){
for(int j=0;j<M;++j){
dfs(i,j);
}
}
Set<Integer> set = new HashSet<>();
for(int i=0;i<N;++i){
for(int j=0;j<M;++j){
set.add(find_parent(i,j));
}
}
bw.write(set.size()+"\n");
bw.flush();
bw.close();
}
}